Raw "Win Rate" is a vanity metric. It’s easily manipulated by betting heavy favorites or claiming wins on stale lines. Here, we use statistical normalization, time-decay weighting, and anomaly detection to separate true edge from variance.
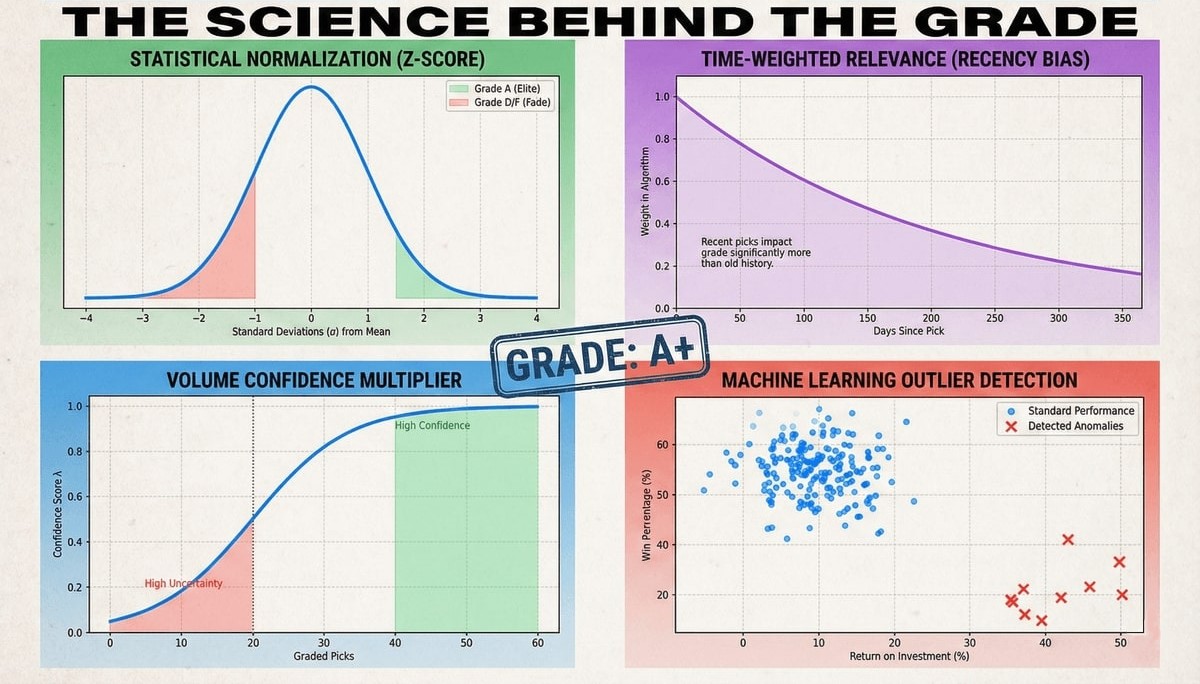
1. Statistical Normalization (Z-Scores)
We normalize data to compare cappers on a level playing field. We convert raw metrics (ROI, Net Units, Win%) into Standard Scores (Z-Scores). This tells us how many standard deviations a capper performs above or below the field average.
If the field average ($\mu$) for ROI is -2% with a standard deviation ($\sigma$) of 5%, a capper with +8% ROI achieves a Z-Score of $+2.0$. This places them in the top 2.5% of the population statistically, regardless of whether they bet on NBA props or NFL sides.
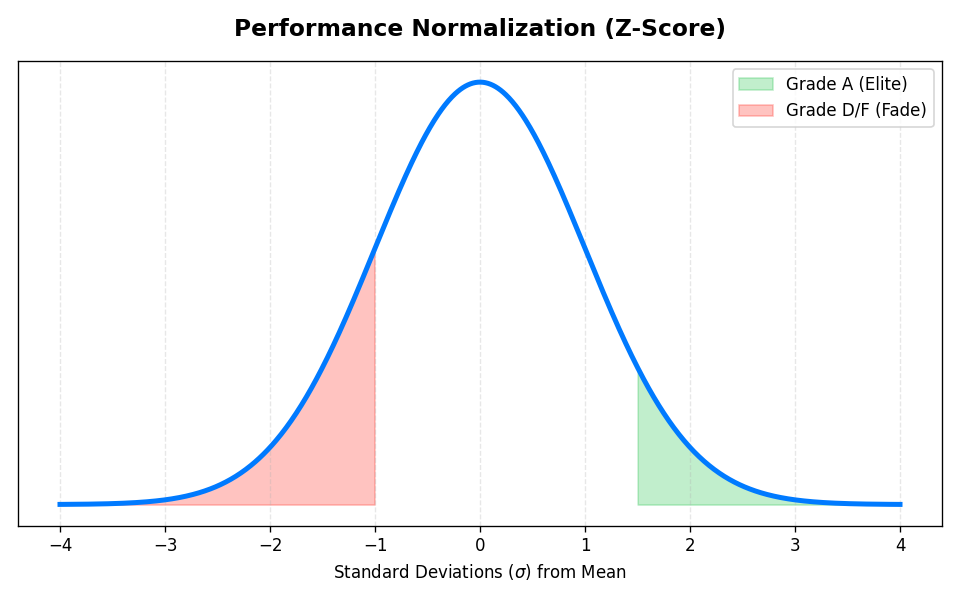
2. Time Decay (Recency Bias)
A capper who crushed the market in 2021 but is losing in 2024 should not have an "A" grade. Markets adapt. To account for this, our algorithm applies a Time Decay Factor to every pick before calculating the aggregate Z-Scores.
We use an exponential decay function where $t$ is the age of the pick in days, and $\lambda$ is the decay constant (currently set to ensure a half-life of ~6 months).
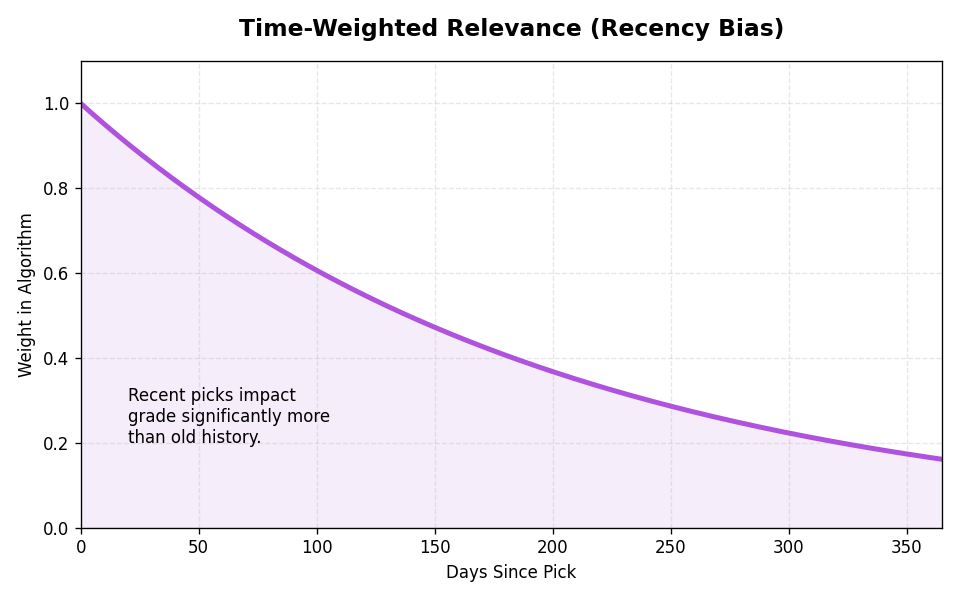
3. The Confidence Multiplier
The "5-0 Problem" is classic in tracking: a new user hits 5 lucky bets and technically has the highest ROI on the site. To prevent them from taking the #1 spot, we apply a Sigmoid Confidence Multiplier ($S(v)$).
This dampens the grade of anyone with low volume. A capper needs a statistically significant sample size (approx. 30+ graded picks) to unlock their full grade potential.
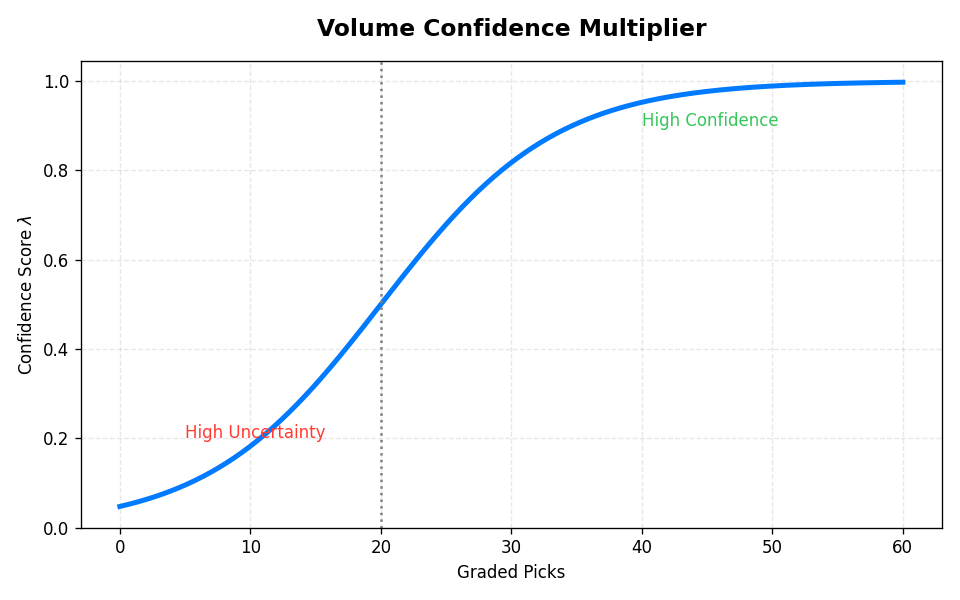
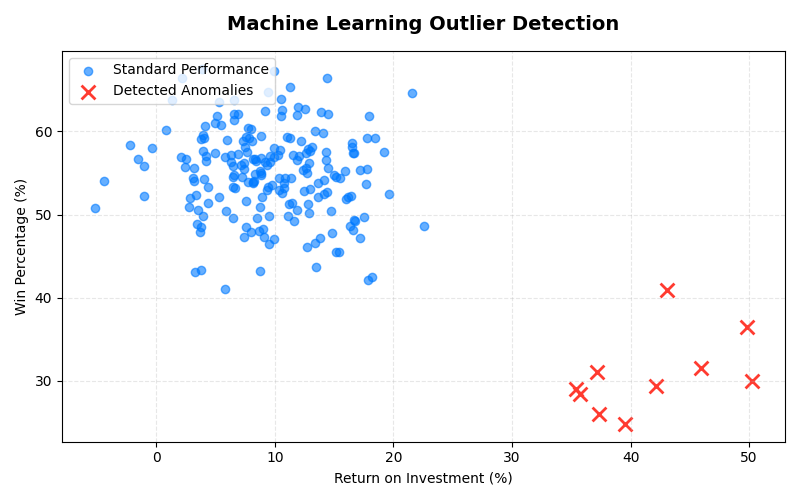
4. Anomaly Detection (Isolation Forest)
Traditional grading can be gamed by "lottery tickets"—betting massive odds on obscure sports to spike ROI. We use an Isolation Forest machine learning model to detect these anomalies.
The model maps every bet into an N-dimensional feature space:
- Feature 1 (Implied Probability): The odds converted to a probability percentage.
- Feature 2 (Unit Variance): Deviation from the user's own average bet size.
- Feature 3 (Sport Liquidity): A weight based on market volume (e.g., NFL > Table Tennis).
Bets that are "isolated" (statistically distant from normal behavior) receive an Anomaly Penalty score. If a capper's profit is driven entirely by these anomalies, their final grade is heavily penalized.
5. Case Study: The Turtle vs. The Hare
Why does ROI alone fail? Consider two real-world examples. Capper A bets recklessly on high-variance parlays. Capper B grinds out small edges consistently. Our algorithm knows the difference.
"The Hare"
ALGORITHM GRADE
Penalized for low volume confidence.
"The Turtle"
ALGORITHM GRADE
Rewarded for proven, long-term edge.
6. How We Determined the Constants (Meta-Optimization)
You might ask: why is the Confidence Midpoint set to 15? Why is ROI weighted at 60%? These numbers were not chosen arbitrarily. They are the result of Machine Learning Backtesting.
We calibrated our model using continuous market data tracked since April 8, 2024. Our objective function was to maximize the Predictive Stability of the grade. In other words, we wanted to find the set of parameters where a "Grade A" capper in Month 1 had the highest probability of remaining profitable in Month 2.
- Grid Search Optimization: We tested thousands of combinations for the weights $w_1$ and $w_2$. We found that weighing ROI higher than Units (0.6 vs 0.4) provided the best correlation with future success.
- Walk-Forward Analysis: To determine the Time Decay $\lambda$, we simulated the grading system moving forward through time. A half-life of ~6 months yielded the most robust rankings that weren't too volatile (changing daily) nor too stale (relying on ancient history).
7. The Final Formula
The final Power Score ($P$) is a weighted aggregate of these components:
This score is then mapped to a percentile rank to assign the final letter grade (A+ to F).
